Presentar las primitivas graficas del M5stack / ESP32

Programar una senoide.

DIbujar las curvas de Lissajous

 

 

	Un M5Stack
	Un cable USB C

 

 

Una gran virtud de M5Stack es llevar incorporado un LCD color de 3 pulgadas normalizado. A diferencia de otros módulos con Arduino o ESP32 no tenemos que comprar adicionalmente un display para poder representar textos y gráficos y además podemos hacerlo desde una serie de librerías gráficas unificadas bastante potables y además fáciles de usar (Que sí. Os lo prometo)

Ya vimos en la sesión anterior que dibujar textos de diferentes tamaños y colores, no tenía mucho secreto. En esta sesión nos vamos a dedicar a los gráficos que podemos representar en la pantalla del M5stack y veréis que es igual de simple que los textos.

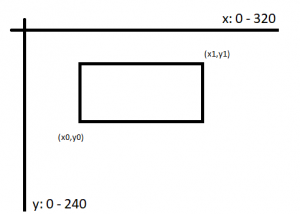
La pantalla es de 320 x 240 puntos en X e Y respectivamente con el origen en la parte superior izquierda:

Eso quiere decir que a medida que Y crece, el punto desciende en la pantalla (No como siempre te contaban en el colegio, que la Y  subía a medida que crecía). Empecemos viendo algunas primitivas básicas disponibles:

M5.Lcd.drawRect(x0, y0, x1, y1, COLOR);
M5.Lcd.fillRect(x0, y0, x1, y1, COLOR);

La primera instrucción dibuja un rectángulo hueco cuya diagonal representan el par de puntos (x0, y0) y (x1, y1) y la segunda dibuja el mismo rectángulo pero lo rellena de color borrando lo que hubiera en el interior

Si quieres borrar la pantalla con un color dado

M5.Lcd.fillScreen( color);

Para dibujar círculos:

M5.Lcd.drawCircle(x0,y0, Radio, color);
M5.Lcd.fillCircle(x0,y0, Radio, color);

Tenemos primitivas para dibujar triángulos y rectángulos con bordes redondeados en incluso una instrucción para mostrar bnitmaps en pantalla

M5.Lcd.drawBitmap

Una buena manera de empezar viendo las primitivas disponibles es abrir el ejemplo de la librería M5

Archivo\ejemplos\M5Stack\Basics\Display

Que despliega un ejemplo de la mayoría de estas funciones

 

 

Tengo la manía, que viene de años atrás, de dibujar una senoide como primer programa  en cualquier pantalla que pillo, para probarla. Y como ya soy muy mayor para cambiar de manías vamos con ello. Lo primero es dibujar los ejes cartesianos:

#include <M5Stack.h>
float k = 2 * 3.1416 /360 ;

void setup()
{  M5.begin();
   M5.Lcd.drawLine( 0,120,320,120,WHITE);
   M5.Lcd.drawLine( 0,0,0,240,WHITE);
}

Como veis incluimos la librería típica de M5 y luego calculamos una constante k, para convertir grados en radianes.

Porque trabajar en radianes es una asco ya que son valores muy pequeños que nos obligarían a usar floats y luego las librerías de M5stack nos obligan a pasarle enteros.

 

Dibujamos un par de líneas rectas como ejes, la primera instrucción dibuja la línea horizontal del eje X (Con Y = 120 para que este en la mitad) y la segunda dibuja el eje Y

Ahora simplemente tenemos que hacer un cálculo de x e y a medida que vamos girando el círculo con la variable i:

void loop()
{  for ( long  i = 0 ; i<360 ; i++)
    {    float x = i * 319/360 ;
         float y= 120 + sin( i * k ) * 120 ;
         M5.Lcd.drawPixel(x,y,BLUE);
     }
}

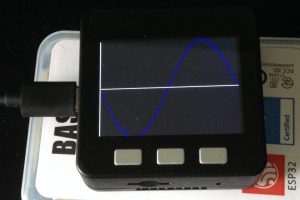
Como veis, el for va aumentando grados entre 0 y 360º, y luego calculamos x como una proporción del ancho de la pantalla y la y con el valor del Seno del ángulo multiplicado por 120 el factor de corrección de altura (Ya que el seno esta entre 0 y 1) y le sumamos 120 para que empiece a dibujar desde media pantalla.

Por último la instrucción M5.Lcd.drawPixel dibuja los puntos en pantalla invertidos, pero no se nota porque la función es simétrica.  M5Stack_Senoide

 

 

Ya sé que cada vez que subimos un poco el nivel, las deserciones se tornan masivas (Especialmente si hablamos de algo que remotamente parezca matemáticas) pero es que no me puedo resistir a sacar provecho del display de M5Stack para ver cómo se ven las curvas de Lisajouss.

Para quienes no hayan disfrutado de los refinados placeres de una educación científica / técnica, podemos comentar que estas curvas son básicamente el producto de un par de ecuaciones paramétricas que producen complejas (Y encantadoras) gráficas, basadas en un par de ecuaciones trigonométricas muy sencillas:

y = cos( p * angulo + fase) ;
x = sin( n * angulo + fase) ;

Donde p, n y fase son los parámetros que podemos ajustar para generar diferentes curvas. Que no se asuste nadie, vamos a ver cómo convertimos esto en un programa de verdad (Fácil, fácil, palabra)

Encabezamos el programa con las inclusiones habituales y un par de definiciones:

#include <M5Stack.h>

byte n = 5 ; byte p = 3 ; byte fase = 0 ;
float k = 2 * 3.1416 / 360 ;

void setup()
{    M5.begin();  }

Incluimos la librería de M5 para habilitar la pantalla y ponemos los parámetros n,p y fase a unos valores iniciales (Que he comprobado genera una gráfica chula) y calculamos k como un factor de conversión de grados a radianes igual que el ejemplo anterior del senoide.

Después tenemos que calcular los puntos que forman la curva así:  M5stack_lissajous

void loop()
{    for ( int i = 0 ; i <= 360 ; i++)
     {   float x = 160 + sin( n * i * k + fase) * 160 ;
         float y = 120 + cos( p * i * k + fase) * 110 ;
         M5.Lcd.drawPixel(x, y, BLUE);
     }
}

Simplemente vamos de 0 a 360º sexagesimales con el for para después calcular los valores x,y de la curva de grado en grado con las instrucciones :

float x = 160 + sin( n * i * k + fase) * 160 ;
float y = 120 + cos( p * i * k + fase) * 120 ;

Conviene destacar que:

Al valor de x sumamos 160, que es la mitad de los 320 puntos que tiene la pantalla para centrar la imagen y lo mismo hacemos con la y, a la que sumamos 120, la mitad de la altura de la pantalla

Por último, como los valores de las funciones seno y coseno están siempre entre 0 y 1, necesitamos multiplicarlas por un factor de escala que de nuevo es la semi anchura y semi altura de la pantalla. O sea para que los puntos se vean y no se salgan de la pantalla.[/fancy-ul] [/three-fourth]

 

Comprendo que entender la idea de Lissajous puede parecer complicado a los no iniciados, pero no me diréis que no es una gráfica chula y que se calcula  con media docenas de líneas (Quien pensaba que era difícil)

Por último, para variar la figura que se nos dibuja, basta con ir asignando valores enteros a n,p y fase. Pero como compilar el programa lleva un buen rato, (Por todas las librerías de M5) sería un poco lata ir cambiando los valores de arriba a mano y recompilar cada vez, por lo que estaría bien asignar valores aleatorios y redibujar cada…. ¿Dos segundos? M5stack_lissajous_random

#include <M5Stack.h>
float k = 2 * 3.1416 / 360 ;

void setup()
{    M5.begin();}

Hasta aquí no hay novedad, y ahora necesitamos generar valores aleatorios para n,p, fase con la función random:

byte n = random(1,6) ;
byte p = random(1,6) ;
byte fase = random(7) * 30 ;

Random genera numero enteros aleatorios entre 0 y el valor que pongamos si solo hay uno, o entre los dos número enteros que le pasamos como parámetros.

Por ejemplo random(1,6) genera valores aleatorios que pueden ser 1,2,3,4,5 pero nunca el 6 (Ojo con esto). En cambio random(7) devuelve valores en 0,1,2,3,4,5,6 nunca 7.

Un comentario particular sobre la fase: Te recomiendo empezar haciendo pruebas con fase =0, esto hará que las figuras sean simétricas y luego prueba con:

byte fase = random(7) * 30 ;

Esto devuelve valores entre 0 y 6 que al multiplicar por 30 te genera: 0,30,60,90,120,150,180.

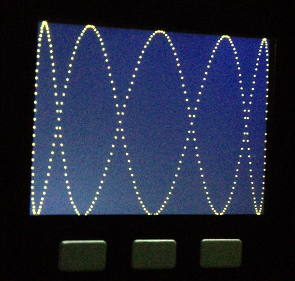
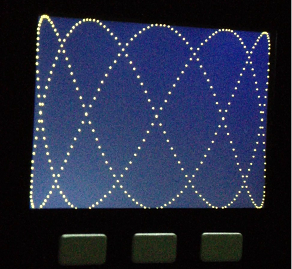
Aquí os dejo algunas fotos  con el resultado:

Los más observadores se habrán percatado que hemos usado la función M5.Lcd.drawPixel(), lo que hace que la imagen sea una nube de puntos y no una línea continua algo que a los puretas desagrada (Dado que es una función continua)y probablemente mis amigos (Los más impresentables) me retirarían el saludo porque esto es poco elegante.

Para corregir este problema bastaría con usar la función  M5.Lcd.drawLine(x0,y0, x1,y1, Color), que me forzaría a guardar el último punto calculado y calcular el primer punto antes de entrar en el loop y quedaria mas o menos así:

Programa:  lissajous_random_line

void loop()
 { byte n = random(1,8) ; 
   byte p = random(2,8) ; 
   byte fase = random(7) * 30 ;

   Xlast = 160 + sin( fase) * 160 ; // Calcular el valor de x0 para i=0
   Ylast = 120 + cos( fase) * 120 ; // Calcular el valor de y0 para i=0
 
   M5.Lcd.fillScreen(BLACK); //Borra la pantalla
   for ( int i = 0 ; i <= 360 ; i++)
       { float x = 160 + sin( n * i * k + fase) * 160 ;
         float y = 120 + cos( p * i * k + fase) * 120 ;
         M5.Lcd.drawLine(Xlast, Ylast,x,y, YELLOW);
         Xlast = x ; Ylast = y ;
       }
   delay (2000);
  }

El resultado lo podéis apreciar en este pequeño video que mi padre describiría como perder el tiempo viendo tonterías en la pantalla en lugar de trabajar como es debido y hacer algo útil: